The purpose of this web page is to preach the gospel about one long run in Markov chain Monte Carlo (MCMC).
If you can't get a good answer with one long run, then you can't get a good answer with many short runs either.Many people reject this, giving a number of different reasons.
There is no reason to believe that m = 1 is optimal, and it generally won't be. So something must be radically wrong with this decision theoretic setup, or the argument is over and ``one long run'' is wrong,
There are two ways to see why this decision theoretic approach is wrong headed.
Many short runs is only ``better'' than one long run when both give rotten answers.If many short runs gives even half decent answers, then the Markov chain mixes fairly well in time n, and one long run will give the same answers as many short runs. So many short runs is only good when it's bad. The answers stink but don't stink quite so much as the answers from one long run. That's supposed be an argument in favor of many short runs?
Here is another way of saying the same thing.
Many short runs isn't MCMC. It's i. i. d. sampling from a slightly fuzzed version of the starting distribution.If mn iterations isn't enough to reach equilibrium, then n isn't even close to enough, and many short runs doesn't sample anything remotely resembling the distribution of interest. So what good is it?
For more on perfect sampling see Gary Wilson's web page on perfect sampling. (The name ``perfect sampling'' is actually due to Wilfrid Kendall. Propp and Wilson called it ``exact sampling.'')
No other ``convergence diagnostic'' can reliably diagnose ``nonconvergence.'' Certainly many short runs cannot.
Many people find this hard to accept. Certainly in toy problems, where you can easily visualize what is going on, it is easy to chose a starting distribution so that many short runs will diagnose nonconvergence. But consider this.
Many short runs can only diagnose nonconvergence when you can quickly get from the starting distribution to every interesting feature of the equilibrium distribution. It only works in toy problems where you already know the answer.If there is an important feature of the equilibrium distribution that cannot be reached with high probability in n steps from a random starting position, then many short runs will fail to detect a catastrophic problem.
A hope of those doing many short runs is that they can choose a starting distribution spread out enough so that it will be near any possible feature of the equilibrium distribution. This hope is forlorn. In a complicated problem with a high-dimensional state space, any starting distribution you can think of is likely to be very far from equilibrium. Hence many short runs is likely to fail as a diagnostic.
But it gets worse.
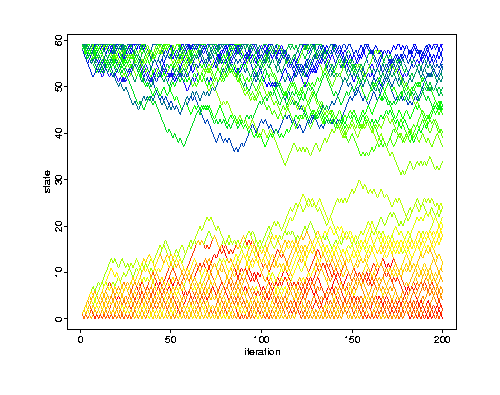
Many short runs can produce false alarms, diagnosing ``nonconvergence'' when n is too short but mn isn't.It's easy to produce toy problems that show this phenomenon. Suppose m = 50 and n = 200, so mn = 10,000. For our toy problem consider a symmetric random walk with reflecting barriers on the integers 1, ..., 60, and consider a starting distribution that has 50% probability of starting at each end.

Here's one long run with mn = 10,000 iterations.
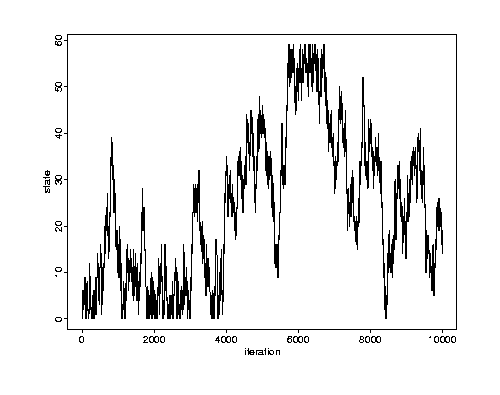
Which is the better ``diagnostic'' here?
Of course, this is irrelevant because of the following
Theorem. All real applications are like the toy problems in which many short runs shines. No real application is like the toy problems in which many short runs sucks.
Proof. Left as an exercise for the many short runs enthusiasts.
No. I do lots of runs. Generally, I've done dozens before the code is even debugged, even more in the testing after the last bug is found. Like everyone else, I generally am interested in many different related probability models. If all have more or less the same behavior, all the runs tell you something about all the models. Usually I do more than one run on a single model, a couple of short ones to figure out how long to run and then a really long run to get some accurate answers.
But published numbers are averages over one long run. The Monte Carlo standard errors are derived from that one run too. That's all I'm recommending.
Shouldn't I worry about getting wrong answers because of ``nonconvergence''? Yes, I do. But I know that bogus diagnostics are no help. If I'm really worried. I try a better sampler. If the best sampler I can think of hasn't converged in the longest runs I have patience to endure, I'm in big trouble. But then nothing will help (short of perfect sampling, but we don't know how to do that yet in most complicated problems).
This is the lamest reason of all. First, it's false. Many referees, editors, and readers can see through woof about diagnostics. You can get papers published with honest restrained claims.
What I can't understand why anyone wants to emit academic weasel wording that decodes to the following
I only implemented one sampling scheme. I couldn't be bothered to figure out any better ones. I tried some so-called diagnostics that are known to fail in hard problems. They didn't show any nonconvergence.In other words, if your problem is so easy that anything would work, you're o. k.
Questions or comments to: Charles Geyer charlie@stat.umn.edu
Back to Charlie Geyer's home page.