


Up: Computer Help
Getting Started with Mathematica
Charles J. Geyer (charlie@stat.umn.edu
)
Mathematica is far too complex for this page to do more than hint at
the possibilities. We just provide a few examples to indicate the
possibilities.
To start Mathematica in command line mode, type math
at a UNIX prompt.
To start Mathematica in notebook mode, type Mathematica
at a UNIX prompt.
To leave Mathematica type Quit at a Mathematica prompt.
In[1]:= Integrate[x^2 Exp[- x], x]
2
-2 - 2 x - x
Out[1]= -------------
x
E
In[2]:= Integrate[x^2 Exp[- x], {x, 0, Infinity}]
Out[2]= 2
In[3]:= Integrate[x^k Exp[- lambda x], {x, 0, Infinity}]
-1 - k
Out[3]= lambda Gamma[1 + k]
In[5]:= D[1 / (1 - t / lambda)^alpha, t]
t -1 - alpha
alpha (1 - ------)
lambda
Out[5]= ----------------------------
lambda
In[6]:= D[1 / (1 - t / lambda)^alpha, {t, 2}]
t -2 - alpha
(-1 - alpha) alpha (1 - ------)
lambda
Out[6]= -(-----------------------------------------)
2
lambda
To define a function of one or more variables, you indicate the
free variables in the function definition by placing an underscore
after the variable name, for example
In[1]:= f[x_] = lambda Exp[ - lambda x]
lambda
Out[1]= ---------
lambda x
E
defines the exponential density function. Then
In[2]:= mu = Integrate[ x f[x], {x, 0, Infinity} ]
1
Out[2]= ------
lambda
In[3]:= sigma2 = Integrate[ (x - mu)^2 f[x], {x, 0, Infinity} ]
-2
Out[3]= lambda
calculate the mean and variance.
For these you have to load a package, either or both of
In[1]:= <<Statistics`ContinuousDistributions`
In[2]:= <<Statistics`DiscreteDistributions`
Among the distributions available are
- Continuous Distributions
- BetaDistribution[
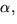
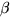 ]
]
- CauchyDistribution[a, b]
- ChiSquareDistribution[n]
- ExponentialDistribution[
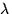 ]
]
- FRatioDistribution[n1, n2]
- GammaDistribution[
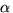 ,
, 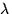 ]
]
- NormalDistribution[
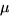 ,
, 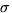 ]
]
- StudentTDistribution[n]
- UniformDistribution[min, max]
- Discrete Distributions
- BinomialDistribution[n, p]
- GeometricDistribution[p]
- HypergeometricDistribution[n,
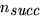 ,
, 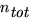 ]
]
- NegativeBinomialDistribution[r, p]
- PoissonDistribution[
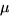 ]
]
Warning: The parameters of these distributions do not always agree
with textbooks. In particular, the 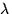 in the gamma distribution is
the reciprocal of the
in the gamma distribution is
the reciprocal of the 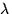 in some textbooks.
in some textbooks.
In[3]:= PDF[GammaDistribution[alpha, lambda], x]
-1 + alpha
x
Out[3]= ----------------------------------
x/lambda alpha
E lambda Gamma[alpha]
Operations on these distributions include
| PDF[dist, x] |
the p. d. f. f(x). |
|---|
| CDF[dist, x] |
the c. d. f. F(x). |
|---|
| Quantile[dist, p] |
the inverse c. d. f. F-1(x). |
|---|
| Mean[dist] |
the mean |
|---|
| Variance[dist] |
the variance |
|---|
| StandardDeviation[dist] |
the standard deviation |
|---|
| Random[dist] |
a random variate |
|---|
Examples
In[3]:= dist = NormalDistribution[2, 3]
Out[3]= NormalDistribution[2, 3]
In[4]:= CDF[dist, -2]
Out[4]= 0.0912112
In[5]:= Quantile[dist, 0.091]
Out[5]= -2.003866860100579
In[6]:= Mean[dist]
Out[6]= 2
In[7]:= StandardDeviation[dist]
Out[7]= 3
In[8]:= Random[dist]
Out[8]= -1.092274190123777
In[9]:= Random[dist]
Out[9]= 0.871083809725889
In[10]:= Table[Random[dist], {5}]
Out[10]= {4.712827641845193, 5.556764945655314, -0.089456940162683,
> 2.668718852551182, 1.822779619000173}
There are also descriptive statistics packages that calculate sample moments.
In[1]:= <<Statistics`DescriptiveStatistics`
In[2]:= data = {2.3, 4.5, 1.03, 17.6}
Out[2]= {2.3, 4.5, 1.03, 17.6}
In[3]:= Mean[data]
Out[3]= 6.3575
In[4]:= StandardDeviation[data]
Out[4]= 7.63085



Up: Computer Help
Charles Geyer
8/10/1999
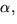
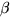 ]
]
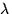 ]
]
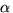 ,
, 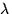 ]
]
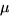 ,
, 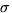 ]
]
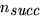 ,
, 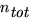 ]
]
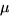 ]
]